引言

“分治”顾名思意：分而治之。《孙子兵法》有云：“凡治众如治寡,分数是也 。”分治法在我们日常生活中也最为常见。比如管理一个国家:先把国家划分为许多省份，再把每个省份划分为若干个市，依此类推，市===》县（区） ===》乡（镇）===》村。这就是分治。在算法设计领域我们有一种算法称为分治算法。

1、分治算法的基本思想及步骤

分治算法的总体设计思想就是”分、治、合“。所对应的步骤也是”分、治、合“。

分：即将一个大的问题依据一种规则分成若干份小的问题。

治：若问题规模足够小，用较简单的方法来解决。若问题规模还是较大则递归调用”分“来继续划分，直至问题规模足够小。

合：按照原问题的要求，将子问题的解按照一定的策略逐层合并，并构成原问题的解。

2、分治算法的适用条件

分治法所能解决的问题一般具有以下几个特征：

1) 该问题的规模缩小到一定的程度就可以容易地解决

2) 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质（很重要）。

3) 利用该问题分解出的子问题的解可以合并为该问题的解（能否用分治法可以说完全取决于这点）；

4) 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子子问题（分治法的效率）。

3、分治算法的时间复杂度

分治算法的时间复杂度分析我们可以用递推公式和递归树。

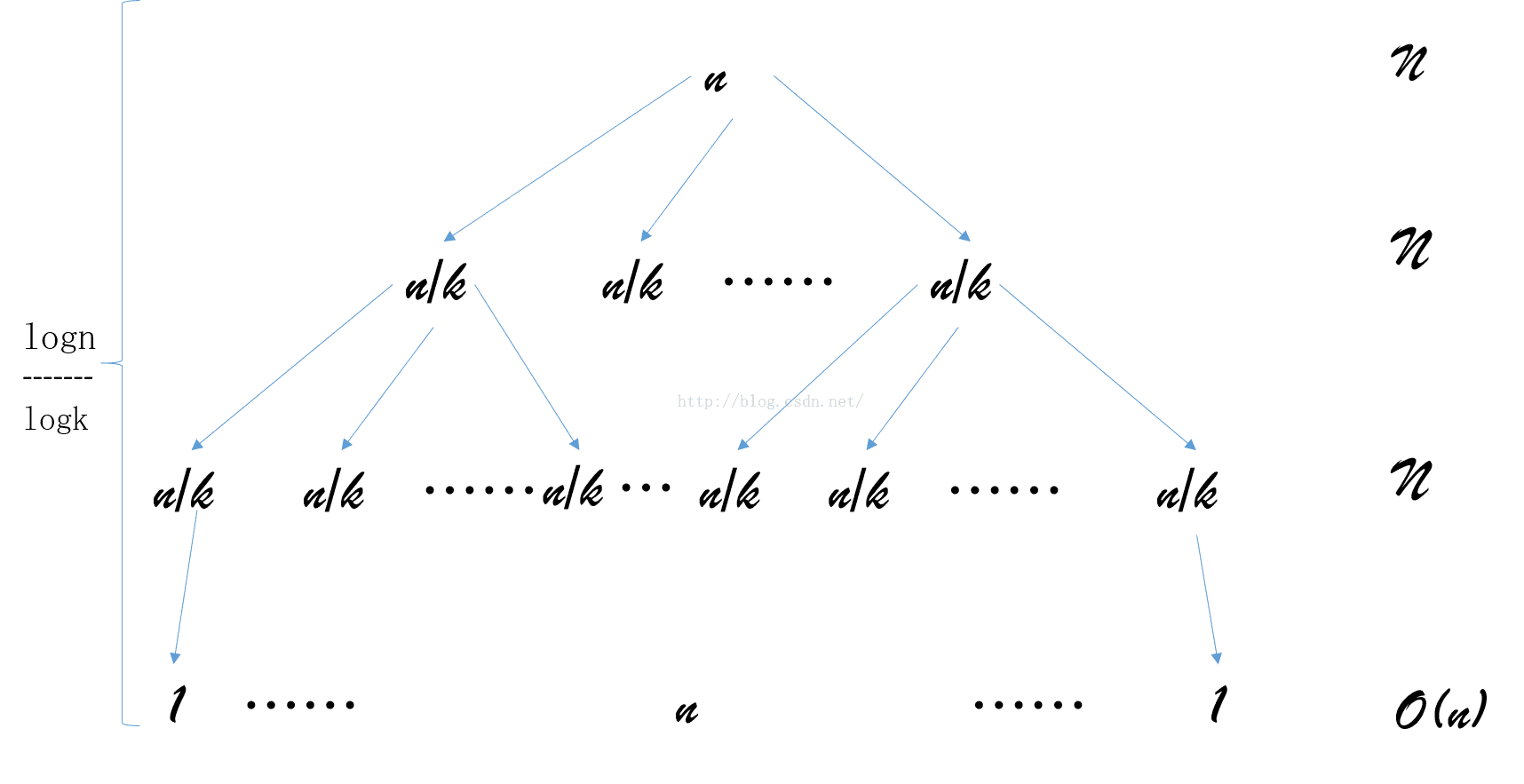
例如：一个规模为n的问题，每次将其分解为k个子问题，直至子问题的规模为1,合并k个子问题的时间复杂度为O(n).

则原问题的时间复杂度T(n)=kT(n/k)+O(n).由此可求得起时间复杂度为 O（nlogn）.

递归树如下：

由于logk为常数，所以可以忽略。则它的时间复杂度为O（n log n).

4、分治算法的经典问题

其中我们最熟悉的莫过于二分搜索及合并排序了。

下面是合并排序的参考代码。

/***************************************   Megre_Sort()* 输入:两个数组及长度*************************************/void Megre_sort(int *A,int p,int *C,int q){	int *B; 	int s=0,t=0,k=0,i = 0,r=p+q;	B = (int *)malloc(sizeof(int)*(p+q));	     while( s <= p && t <= q )		 	 {		 if(A[s] <= C[t])		 {			 B[k] = A[s];			 s++;		 }		 else		 {			 B[k] = C[t];			 t++;		 }		 k++;	 }	 if (s = q +1)		 for( i = 0; i <= (r-k);i++)			 B[k+i] = C[t+i];		 else			 for( i = 0; i <= (r-k);i++)			 B[k+i] = A[s+i];for(i = 0; i < p+q ; i++){	printf("%d ",B[i]);}}/***************************************   BottomUp_Sort()* 输入:数组及长度*************************************/void BottomUp_Sort(int n){	int i = 1,s,j;	int *A;	A = (int*)malloc(sizeof(int)*n);   srand( (unsigned)time( NULL ) );     for(i = 0;i < n; i ++)   {	   A[i] = rand();   }    while ( i < n)	{ 		s = i;		i = 2*s;		j = 0;		while ( j + i <= n)		{			Megre_sort(A,s,A+s,i);			j++;		}		if ( j + s < n)			Megre_sort(A,s,A+s,n-j);	}}

快速排序参考代码：

/***************************************       Quick_Sort()* 输入:数组及长度*************************************/void Quick_Sort(int *A,int low,int high){	    if (A == NULL || low >= high)        return ;    int part = SPLIT(A, low, high);    Quick_Sort(A, low, part-1);    Quick_Sort(A, part+1, high);       }/***************************************       SPLIT()* 输入:划分数组 *************************************/int SPLIT(int *a, int beg, int end){    int i,c,x,j;         i = beg;         x = a[beg];        for(j = beg+1; j <= end; ++j)        {            if(a[j] <= x)            {			     ++i;			     if(i != j)			     {    				c= a[i];				  a[i]=a[j];				  a[j] =c;     			 }                }        }        x = a[beg];		 a[beg]=a[i];		 a[i] = x;        return i;}